MatheAss 10.0 − Algebra

Prime numbers

The program calculates all prime numbers between two numbers.

Prime numbers between 1000000000 and 1000000300:

1000000007 1000000009 1000000021 1000000033 1000000087 1000000093
1000000097 1000000103 1000000123 1000000181 1000000207 1000000223
1000000241 1000000271 1000000289 1000000297

16 prime numbers

Prime tuples (New in version 9.0)

The program determines all prime number twins (p, p + 2), prime number cousins (p, p + 4), sexy primes (p, p + 6) and prime number triplets in an interval [a, b].

Prime triplets between 1 and 200

(3 | 5 | 7) (5 | 7 | 11) [7 | 11 | 13] (11 | 13 | 17) [13 | 17 | 19] (17 | 19 | 23) [37 | 41 | 43] 
(41 | 43 | 47) [67 | 71 | 73] [97 | 101 | 103] (101 | 103 | 107) [103 | 107 | 109] (107 | 109 | 113)
(191 | 193 | 197) [193 | 197 | 199] 

15 prime triplets
7 of the form (p | p + 2 | p + 6) and 7 of the form [p | p + 4 | p + 6]

Prime factorization

The program breaks down natural numbers into their prime powers.

  99999999999901 = 19001 5262880901
  99999999999001 = 107 401 1327 1756309
  99999999990001 = prime number 
    3938980639167 = 3 ¹⁴ 7 ⁷ 
999330136292431 = 99971 ² 99991

GCD and LCM

For two numbers a and b, the greatest common divisor, the least common multiple and their subsets are determined.

a = 24
b = 256

greatest common factor gcd = 8
lowest common multiple lcm = 768  

Subsets:
T(a) = { 1 2 3 4 6 8 12 24}
T(b) = { 1 2 4 8 16 32 64 128 256}

Calculating percentages (new in version 9.0)

The base value G, the percentage value W, the percentage p or p%, the growth factor q and the final value E are calculated if two independent values are entered.

Given:
¯¯¯¯¯¯¯¯
        Percentage value W = −120
Growth factor q = 95% = 0.95 = 19/20

Results:
¯¯¯¯¯¯¯¯¯¯
          Basic value G = 2400
     Percentage p% = −5% = −0.05 = −1/20      
              End value E = 2280

Decimal numbers into fractions

The program converts periodic and terminating decimal fractions into fractions.

Non-periodic part: 1.20
Period: 045
    ___
1.20045 = 120/100 + 1/2220 = 533/444

Fractions into decimals

The program converts fractions into periodic decimal fractions and determines the period and its length.

numerator   : 533
denumerator : 444
              ___
533/444 = 1.20045

The recurring decimal starts with the
3rd digit following the decimal point
and is 3 digits long.

Binomials of n-th Degree

The binomial formula (a + b)² = a² + 2ab + b² is certainly one of the best-known formulas in school mathematics.

The program calculates the more general case (a·x + b·y)ⁿ.

(2·x - 3·y)⁷ =       +128·x⁷
                         −1344·x⁶ · y
                         +6048·x⁵ · y²
                       −15120·x⁴ · y³   
                       +22680·x³ · y⁴
                       −20412·x² · y⁵
                       +10206·x · y⁶
                         −2187·y⁷

The program determines the real-valued solutions of an equation of 4th or smaller degree. For equations of a higher degree there is no algebraic solution method apart from approximate calculations (zeros in the program Calculus of Arbitrary Functions).

x⁴ + 2·x³ - 3·x² + 5·x - 5 = 0   <=>   (x - 1)·(x³ + 3·x² + 5) = 0
L = {-3,42599;  1}

Diophantine Equations

The program computes the integer solutions of the equation a·x - b = m·y with m>0.
This for example permits the determination of the integer points in a straight line.

7·x − 3·y − 5 = 0 ;   x,y integer
L = { ( 2 + 3t | 3 + 7t ) }

Pythagorean triples

Pythagorean triples are the integer solutions (x, y, z) of the equation x² + y² = z², which applies to the sides in right triangles.

For x, y, z between 100 and 400 we get:

( 119, 120, 169 )    ( 104, 153, 185 )    ( 133, 156, 205 )    ( 105, 208, 233 )    
( 140, 171, 221 )    ( 115, 252, 277 )    ( 120, 209, 241 )    ( 161, 240, 289 )    
( 160, 231, 281 )    ( 207, 224, 305 )    ( 175, 288, 337 )    ( 135, 352, 377 )    
( 136, 273, 305 )    ( 204, 253, 325 )    ( 225, 272, 353 )    ( 189, 340, 389 )    
( 180, 299, 349 )    ( 252, 275, 373 )    ( 152, 345, 377 )    ( 228, 325, 397 )

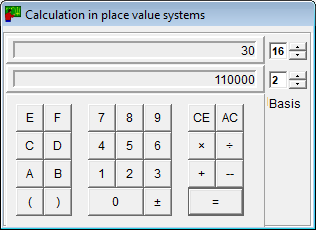
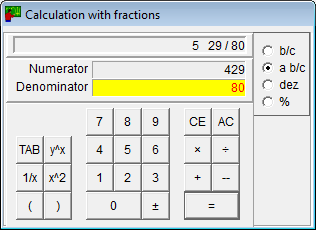
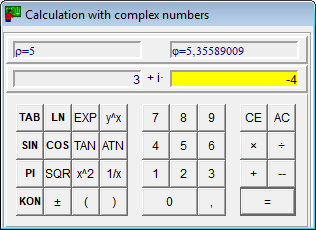
Calculators

The calculator for fractions can do the four basic arithmetic operations and can raise fractions to the power.
The calculator for place value systems works with every base between 2 and 16.
In addition to the usual functions, the calculator for complex numbers also calculates the conjugate complexes of a number.

Calculating with large numbers (new in version 9.0 from April 2021)

The calculation is based on whole numbers with a maximum of 10,000 digits.

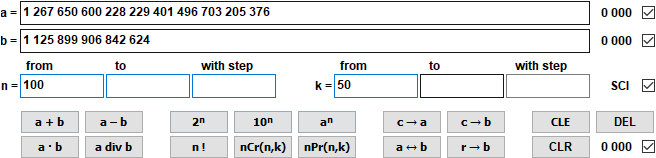
1 267 650 600 228 229 401 496 703 205 376 div 1 125 899 906 842 624  
 =  1 125 899 906 842 624  Remainder  0
 =  1,13 · 10^15 Remainder 0

nCr(100,50)  =  100 891 344 545 564 193 334 812 497 256 = 1,01 · 10^29

eng.matheass.eu