MatheAss 10.0 - Linear Algebra

Systems of linear equations

The program determines the solution vector from a system of linear equations with n equations and n unknowns.

Example: Looking for a parabola through the points P (1|3), Q (2|1) and R (4|9) leads to the system of equations

  1·x1 + 1·x2 + 1·x3 = 3
  4·x1 + 2·x2 + 1·x3 = 1
 16·x1 + 4·x2 + 1·x3 = 9   
            
 L = (2; -8; 9)

So the parabola has the equation y = 2x ² - 8x + 9.

Example with two-dimensional Solution space:

  0·x1 + 0·x2 + 2·x3 - 1·x4  =  1
  1·x1 + 1·x2 + 1·x3 + 1·x4  =  4
  2·x1 + 2·x2 - 4·x3 + 5·x4  =  5
  1·x1 + 1·x2 - 7·x3 + 5·x4  =  0

  L = { ( 3,5-s-1,5t; s; 0,5+0,5t; t ) | s,t ∈ R }

Linear Optimization (since February 2022)

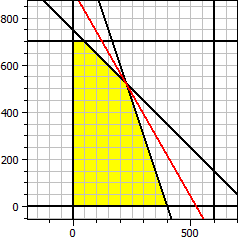
The program determines the optimal solution for a two-variable objective function with linear inequalities as constraints.

Objective function:
  ƒ(x,y) = 140·x + 80·y → Maximum

Constraints:
  x ≥ 0
  y ≥ 0
  x ≤ 600
  y ≤ 700
  x + y ≤ 750
  3·x + y ≤ 1200

Maximum:
  x = 225   y = 525
  ƒ(x,y) = 73500

The program determines the linear combination of a vector from three given vectors. The routine is also suitable for checking the linear independence of three vectors in space, i.e. whether they lie in one plane.


    ⎧ 1 ⎫     ⎧ 1 ⎫     ⎧ 1 ⎫   ⎧ 2 ⎫
  a·⎪ 0 ⎪ + b·⎪ 1 ⎪ + c·⎪ 1 ⎪ = ⎪ 3 ⎪
    ⎩ 0 ⎭     ⎩ 0 ⎭     ⎩ 1 ⎭   ⎩ 4 ⎭

 Solution:
     a = -1  b = -1  c = 4

Scalar product

The program calculates the scalar product of two vectors, the length of the two vectors and the included angle.


   ->  ⎧ 1 ⎫     ->  ⎧ 5 ⎫
   a = ⎪ 3 ⎪     b = ⎪ 0 ⎪
       ⎩ 1 ⎭         ⎩ 3 ⎭
           
Scalar product of the vec.  = 8

Length of the first vector  = √11 = 3.32

Length of the second vector = √34 = 5.83

included angle            α = 65.56°

Vector product

The program calculates the vector product and its amount for two vectors. The vector product is perpendicular to the parallelogram spanned by you, and its amount is equal to the area of the parallelogram.


     ->  ⎧ 1 ⎫     ->  ⎧ 7 ⎫
     a = ⎪ 2 ⎪     b = ⎪ 1 ⎪
         ⎩ 3 ⎭         ⎩ 4 ⎭

 ->  ->  ⎧  5 ⎫    ->  ->  
 a x b = ⎪ 17 ⎪   |a x b|= √483 = 21,977261
         ⎩-13 ⎭

Triple Product

The program calculates the late product for three vectors. Its amount indicates the volume of the displaced cuboid (spatula) that is spanned by the three vectors.


->  ⎧ 2 ⎫     ->  ⎧ 2 ⎫    ->  ⎧ 3 ⎫
a = ⎪ 3 ⎪     b = ⎪-1 ⎪    c = ⎪ 9 ⎪
    ⎩ 5 ⎭         ⎩ 7 ⎭        ⎩ 2 ⎭

  ->  ->    ->  
( a x b ) · c = 26

Matrix Inversion

The program calculates the determinant, the rank and the inverse matrix for a square matrix of order n.

Matrix :        
¯¯¯¯¯¯¯¯
  ⎧ 1  0  2 ⎫
  ⎪ 0  1  0 ⎪
  ⎩ 3  0  1 ⎭

Inverse Matrix :
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
  ⎧-0,2  0  0,4 ⎫
  ⎪   0  1    0 ⎪
  ⎩ 0,6  0 -0,2 ⎭

Order = 3,  Rank = 3,  Determinant = -5

Pseudoinverse Matrix

If the columns of a matrix A are linearly independent, then A ^T A is invertible and the pseudo inverse is obtained with the following formula:

A⁺ = ( A^T· A )^-1· A^T

It is A ⁺ is a left inverse of A , that is, it applies: A ⁺ * A = E .

Matrix A
¯¯¯¯¯¯¯¯
  ⎧ 1  1  1  1 ⎫
  ⎩ 5  7  7  9 ⎭

A^T· A
¯¯¯¯¯
  ⎧ 26  36  36  46 ⎫
  ⎪ 36  50  50  64 ⎪
  ⎪ 36  50  50  64 ⎪
  ⎩ 46  64  64  82 ⎭

A^T· A is not invertible

A · A^T
¯¯¯¯¯¯
  ⎧  4   28 ⎫
  ⎩ 28  204 ⎭

( A · A^T )^-1
¯¯¯¯¯¯¯¯¯¯¯¯
  ⎧ 6,375 -0,875 ⎫
  ⎩-0,875  0,125 ⎭

Right Inverse:  A^T·( A·A^T )^-1
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
  ⎧    2 -0,25 ⎫
  ⎪ 0,25     0 ⎪
  ⎪ 0,25     0 ⎪
  ⎩ -1,5  0,25 ⎭

Matrix Multiplication

The program calculates the product matrix for two matrices.

1. Matrix :     
¯¯¯¯¯¯¯¯¯¯
  ⎧ 1  0  2 ⎫
  ⎩ 0  1  0 ⎭

2. Matrix :     
¯¯¯¯¯¯¯¯¯¯
  ⎧-0,2  0  0,4  1 ⎫
  ⎪   0  1    0  1 ⎪
  ⎩ 0,6  0 -0,2  1 ⎭

Product Matrix:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
  ⎧ 1  0  0  3 ⎫
  ⎩ 0  1  0  1 ⎭

MatheAss 10.0 - Linear Algebra

A+ = ( AT· A )-1· AT

A⁺ = ( A^T· A )^-1· A^T