MatheAss 10.0 - Analysis
Sequences and Series (New in version 9.0 from May 2021)
The program determines the first n members of a sequence (ai) and the corresponding series (sum of the sequence members) if the first limbs of the sequence and an explicit function ai=ƒ(i) or a recursion formula ai=ƒ(a0, a1, ... , ai-1) are given.
Sequence ¯¯¯¯¯¯¯¯ ( a[ i ] ) = (1; 3; 5; 7; 9; 11; 13; 15; 17; 19) Serie ¯¯¯¯ ( Σ a[ i ] ) = (1; 4; 9; 16; 25; 36; 49; 64; 81; 100)
Division of Polynomials
The program calculates the product and the quotient of two polynomials.
1st polynomial: 3·x4 - 2 x + 1
2nd polynomial: 2·x + 5
Product: 6·x5 + 15·x4 - 4·x2 - 8·x + 5
Quotient: 3/2·x3 - 15/4·x2 + 75/8·x - 391/16
Remainder: 1971/16
Factoring Polynomials (New in version 9.0)
p(x) = x5 - 9·x4 - 82/9·x3 + 82·x2 + x - 9
= (1/9)·(9·x5 - 81·x4 - 82·x3 + 738·x2 + 9·x - 81)
= (1/9)·(3·x - 1)·(3·x + 1)·(x - 9)·(x - 3)·(x + 3)
Rational zeros: 1/3, -1/3, 9, 3, -3
Transforming Polynomials (New in Version 9.0)
A polynomial function ƒ(x) can be shifted or stretched in the x direction and y direction.
ƒ(x) = - 1/4·x4 + 2·x3 - 16·x + 21 Shifted by dx = -2, dy = 0 ƒ(x + 2) = - 1/4 ·x4 + 6 ·x2 + 1
Polynomials GCD and LCM (new in version 9.0 from February 2021)
The program calculates the greatest common divisor (GCD) and the least common multiple (LCM) of two polynomials p1(x) and p2(x).
p1(x) = 4·x6 - 2·x5 - 6·x4- 18·x3 - 2·x2 + 24·x + 8 p2(x) = 10·x4- 14·x3 - 22·x2 + 14·x + 12 GCD(p1,p2) = x2 - x - 2 LCM(p1,p2) = 40·x8 - 36·x7 - 76·x6 - 144·x5 + 88·x4+ 356·x3 - 4·x2 - 176·x - 48
 Function Plotter
Function Plotter
Up to ten functions can be drawn simultaneously in a coordinate system. Links or derivatives of already defined functions are also permitted.
If ƒ1(x) = sin(x) and ƒ2(x) = 3*sqrt(x), then ƒ3(x) = 2*y1^2-y2 substitudes ƒ3(x) = 2*sin(x)^2-3*sqrt(x) ƒ4(x) = f2(y1) substitudes ƒ4(x) = 3*sqrt(sin(x)) ƒ5(x) = y2' substitudes ƒ5(x) = 3/(2*sqrt(x))
Example: ƒ1(x)=sin(x), ƒ2(x)=x and ƒ3(x)=y1+y2
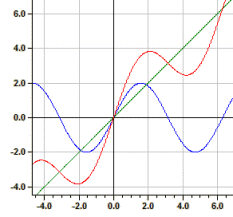
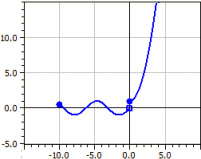
 Piecewise Functions
Piecewise Functions
A function defined in sections is drawn, which is given by up to nine subfunctions. For each of the subfunctions, the definition area, the type of interval, and the color are entered. It is also possible to determine whether the boundary points are drawn or not.
Example:
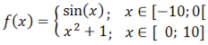
 Parameter curves
Parameter curves
With this program, curves can be drawn that are not given by an explicit function term, but by two functions for horizontal and vertical deflection.
Example: Lissajou figures
x(k) = sin(3*k)
y(k) = cos(5*k)
k from -Pi to Pi
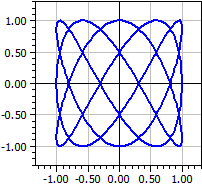
Des figures de Lissajou sont obtenus lorsque deux tensions alternatives de fréquences différentes sont appliquées à un oscilloscope.

Lissajou figures are obtained when two a-c voltages with different frequencies are applied to an oscilloscope.
 Family of Curves
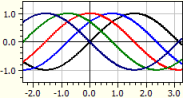
Family of Curves
The program draws the graphs of any function that contains a blade parameter k. The values for k can be listed or determined by initial value, end value and step size.
ƒ(x,k) = sin(x+k)
k from -2 to 2 with step size Pi/4
 Calculus of Polynomial Functions
(New in Version 9.0)
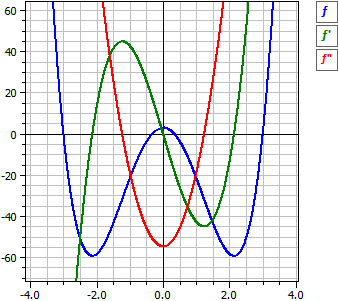
Calculus of Polynomial Functions
(New in Version 9.0)
The program performs the curve discussion for a polynomial function. That is, the derivatives and the root function (antiderivative) are determined, the function is examined for rational zeros, extremes, turning points and symmetry.
Function:
¯¯¯¯¯¯¯¯
ƒ(x) = 3·x4 - 82/3·x2 + 3
= 1/3·(9·x4 - 82·x2 + 9)
= 1/3·(3·x - 1)·(3·x + 1)·(x - 3)·(x + 3)
Derivations:
¯¯¯¯¯¯¯¯¯¯
ƒ'(x) = 12·x3 - 164/3·x
ƒ"(x) = 36·x2 - 164/3
ƒ'"(x) = 72·x
Antiderivative:
¯¯¯¯¯¯¯¯¯¯¯
F(x) = 3/5·x5 - 82/9·x3 + 3·x + c
.
.
.
 Calculus of Rational Functions
(New in Version 9.0)
Calculus of Rational Functions
(New in Version 9.0)
The program performs the curve discussion for a rational function. That is, the derivatives, the definition gaps and the continuous continuation are determined. The function is examined for zeros, extrema, turning points, and behavior for |x|→ ∞.
Function :
¯¯¯¯¯¯¯¯
3·x3 + x2 - 4 (x - 1)·(3·x2 + 4·x + 4)
ƒ(x) = —————— = ———————————
4·x2 - 16 4·(x - 2)·(x + 2)
Singularities:
¯¯¯¯¯¯¯¯¯¯¯
x = 2 Pole with change of sign
x =-2 Pole with change of sign
Derivatives:
¯¯¯¯¯¯¯¯¯¯
3·(x4 - 12·x2) 3·(x2·(x2 - 12))
ƒ'(x) = ———————— = ————————
4·(x4 - 8·x2 + 16) 4·(x - 2)2·(x + 2)2
6·(x3 + 12·x) 6·(x·(x2 + 12))
ƒ"(x) = ——————————— = ———————
x6 - 12·x4 + 48·x2 - 64 (x - 2)3·(x + 2)3
.
.
.
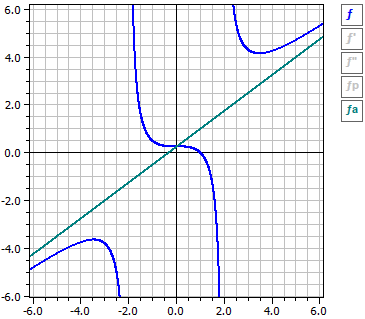
 Calculus of arbitrary Functions
Calculus of arbitrary Functions
The program performs the curve discussion for any function. That is, the derivatives are determined, the function is examined for zeros, extrema and turning points, the graphs of ƒ, ƒ' and ƒ" are drawn, and a table of values is output.
Function: ‾‾‾‾‾‾‾‾‾‾‾‾ ƒ(x) = x^4-2*x^3+1 Examination in the range from -10 to 10 Derivations: ‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾ ƒ'(x) = 4*x^3-6*x^2 ƒ"(x) = 12*x^2-12*x Zeros: ‾‾‾‾‾‾‾‾ N1(1|0) m = - 2 N2(1,83929|0) m = + 4,5912 Extremes: ‾‾‾‾‾‾‾‾‾‾‾‾‾ T1(1,5|-0,6875) m = 0 Pts of inflection: ‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾ W1(0|1) m = + 0 W2(1|0) m = - 2
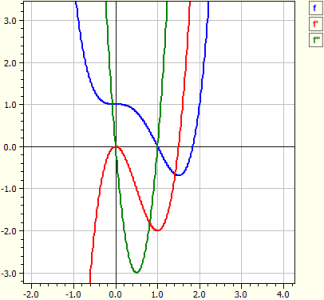
 Newton Iteration
Newton Iteration
Newton iteration is an approximation method for calculating a zero of ƒ(x). If you enter a starting value x0 that is close enough to the desired zero, the next approximation is the intersection of the tangent to the graph of f in the point
ƒ(x) = x-cos(x)
x ƒ(x) ƒ'(x)
———————— —————— ——————
x0 = 1
x1 = 0,75036387 0,45969769 1,841471
x2 = 0,73911289 0,018923074 1,681905
x3 = 0,73908513 0,00004646 1,6736325
x4 = 0,73908513 0,00000000 1,673612
 Integral Calculus (from February 2021 with arc lengths)
Integral Calculus (from February 2021 with arc lengths)
The oriented and absolute contents of the surface between two function curves are calculated at a desired interval [a; b].
In addition the twisting moments for rotation, the bodies of revolution and the arc lengths in the interval.
ƒ1(x) = cosh(x) ƒ2(x) = x^2+1 Limits of integration from -2 to 2 Oriented content : A1 = -2,07961 Absolute content : A2 = 2,07961 Arc lengths : L1[a;b] = 7,254 L2[a,b] = 9,294
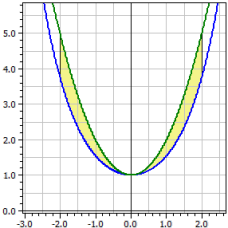
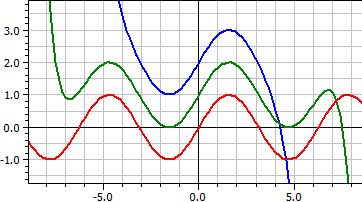
 Series Development
Series Development
A function given as a series is drawn, whereby the series developments for different parameter ranges can be compared and moved in the y-direction for better differentiation.
The first 16 members of the Taylor series for the sine function. . ƒ(x,k) = x^(2*k-1)/fac(2*k-1)*(-1)^(k+1) , k = 4, 8 und 16
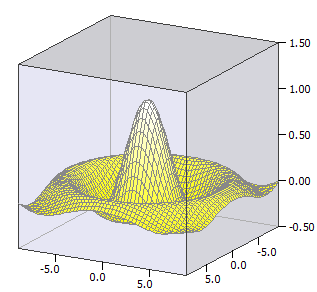
 Surface Functions
Surface Functions
A surface function ƒ(x,y), i.e. the three-dimensional diagram of a function with two variables, is drawn.
Example:
ƒ(x, y) = sin(u) / u
u(x, y) = sqrt(x * x + y * y)
-9 ≤ x ≤ 9
-9 ≤ y ≤ 9;
-0,5 ≤ z ≤ 1,5